Jackson's theorem (queueing theory)
In queueing theory, a discipline within the mathematical theory of probability Jackson's theorem is a theorem by James R. Jackson.[1] It was the first significant development in the theory of networks of queues, and generalising and applying the ideas of the theorem to search for similar product form solutions in other networks has been the subject of much research,[2] including ideas used in the development of the Internet.[3] The paper was re-printed in the journal Management Science’s ‘Ten Most Influential Titles of Management Sciences First Fifty Years.’[4]
Jackson was inspired by the work of Burke and Reich,[5] though Walrand notes "product form results … [are] a much less immediate result of the output theorem than Jackson himself appeared to believe in his fundamental paper".[6]
An earlier product form solution was found by R. R. P. Jackson for tandem queues (a finite chain of queues where each customer must visit each queue in order) and cyclic networks (a loop of queues where each customer must visit each queue in order).[7]
Contents |
Definition of a Jackson network
A network of m interconnected queues is known as a Jackson network[8] or Jacksonian network[9] if it meets the following conditions:
- the network is open and any external arrivals to node i form a Poisson process,
- all service times are exponentially distributed and the service discipline at all queues is FCFS,
- a customer completing service at queue i will either move to some new queue j with probability
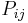 or leave the system with probability
or leave the system with probability 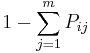 , which is non-zero for some subset of the queues,
, which is non-zero for some subset of the queues, - the utilization of all of the queues is less than one.
Theorem
In an open Jackson network of m M/M/1 queues where the utilization 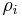 is less than 1 at every queue, the equilibrium state probability distribution exists and for state
is less than 1 at every queue, the equilibrium state probability distribution exists and for state 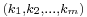 is given by the product of the individual queue equilibrium distributions
is given by the product of the individual queue equilibrium distributions
The result 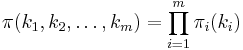 also holds for M/M/c model stations with ci servers at the
also holds for M/M/c model stations with ci servers at the 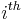 station, with utilization requirement
station, with utilization requirement 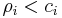 .
.
Generalized Jackson network
A generalized Jackson network allows renewal arrival processes that need not be Poisson processes, and independent, identically distributed non-exponential service times. In general, this network does not have a product form stationary distribution, so approximations are sought.[10]
See also
Notes
- ^ Jackson, James R. (Oct. 1963). "Jobshop-like Queueing Systems". Management Science 10 (1): 131–142. doi:10.1287/mnsc.1040.0268. JSTOR 2627213.
- ^ Kelly, F. P. (Jun. 1976). "Networks of Queues". Advances in Applied Probability 8 (2): 416–432. JSTOR 1425912.
- ^ Jackson, James R. (December 2004). Comments on "Jobshop-Like Queueing Systems": The Background. 50. pp. 1796–1802. JSTOR 30046150.
- ^ Jackson, James R. (December 2004). Jobshop-Like Queueing Systems. 50. pp. 1796–1802. JSTOR 30046149.
- ^ Reich, Edgar (September 1957). "Waiting Times When Queues are in Tandem". Annals of Mathematical Statistics 28 (3). doi:10.1214/aoms/1177706889. JSTOR 2237237.
- ^ Walrand, Jean (November 1983). "A Probabilistic Look at Networks of Quasi-Reversible Queues". IEEE Transactions on Information Theory 29 (6). doi:10.1109/TIT.1983.1056762.
- ^ Jackson, R. R. P. (1995). "Book review: Queueing networks and product forms: a systems approach". IMA Journal of Management Mathematics 6 (4): 382–384. doi:10.1093/imaman/6.4.382.
- ^ Goodman, J. B.; Massey, W. A. (1984). "The Non-Ergodic Jackson Network". Journal of Applied Probability 21 (4): 860–869. doi:10.2307/3213702.
- ^ Walrand, J.; Varaiya, P. (1980). "Sojourn Times and the Overtaking Condition in Jacksonian Networks". Advances in Applied Probability 12 (4): 1000–1018. doi:10.2307/1426753.
- ^ Chen, Hong; Yao, David D. (2001). Fundamentals of Queueing Networks: Performance, Asymptotics, and Optimization. Springer. ISBN 0387951660.
![\pi (k_1,k_2,\ldots,k_m) = \prod_{i=1}^{m} \pi_i(k_i) = \prod_{i=1}^{m} [\rho_i^{k_i} (1-\rho_i)].](/2012-wikipedia_en_all_nopic_01_2012/I/e0e32641e8ca34881de8e80b73acbbf1.png)